
🔧 모델링 - 데이터 생성 / 인코딩
(예측 모델링에 사용할 컬럼들을 설정하여 새로운 데이터프레임 생성)
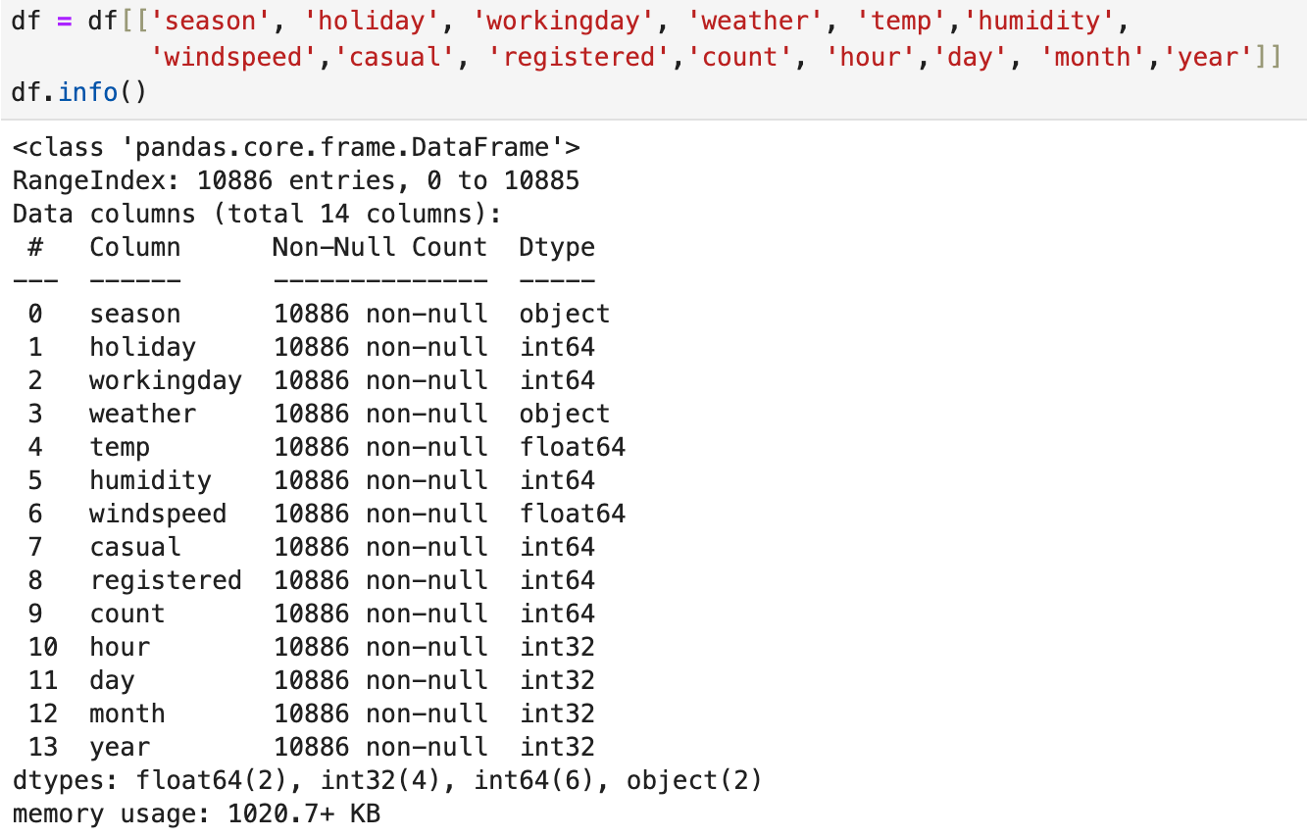
(컬럼별로 unique값 확인하기)

(원-핫 인코딩_One-Hot Encoding)
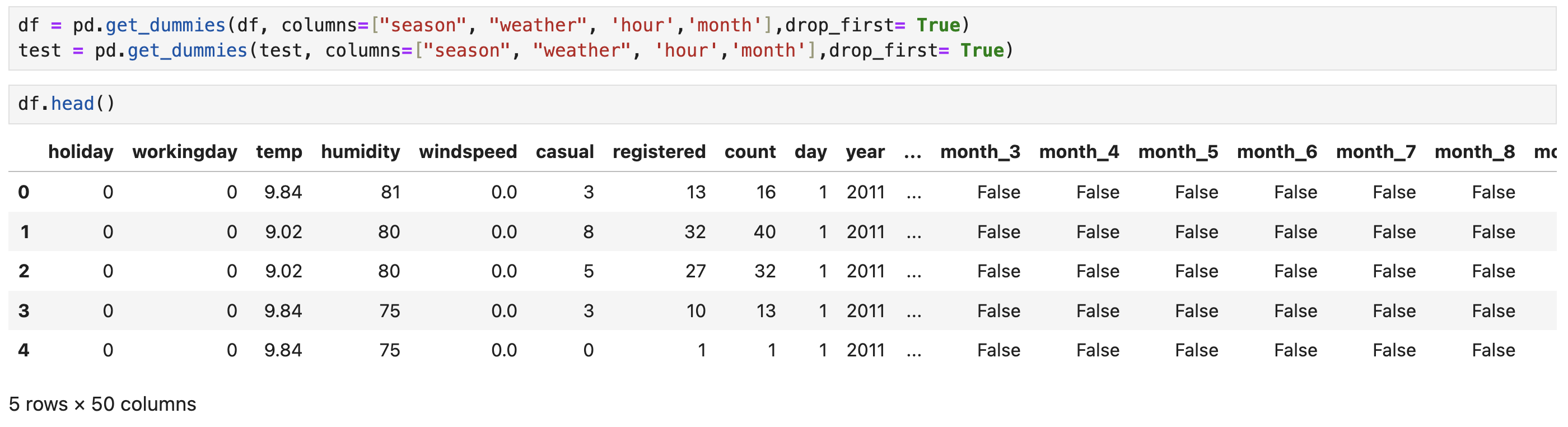
: 머신러닝 알고리즘은 숫자 데이터만 처리할 수 있기에 원-핫 인코딩(One-Hot Encoding)을 해야 한다. 또한 원-핫 인코딩은 범주형 데이터를 효과적으로 변환하는 방법이기도 하다. 이는 머신러닝 모델의 정확도를 높이고 학습 효율성을 향상시키는 중요한 전처리 과정이다.
🔧 모델링 - 데이터 분리 / 스케일링
(독립변수(X)와 종속 변수(y) 분리)

- X : 10886개의 샘플 개수 / 47개의 특성(2D)
- y : 10886개의 샘플 개수(1D)
(스케일링)

: 표준화는 sklearn.preprocessing의 StandardScaler를 사용하여 수행한다.
→ 표준화 시, 동일한 범위를 가지게 되어 모델이 특정 변수에 의존하는 현상을 방지 가능.
| ✔ MinMaxScaler 대신 StandardScaler를 선택한 이유 → 사용할 데이터는 이상치가 존재하는 변수도 포함되어 있기에 이상치에 덜 민감한 StandardScaler을 선택하였다. → StandardScaler : 평균 = 0, 표준편차 = 1 로 변환 |
(train / test 데이터 분리)

🔧 모델링 - 평가 지표 함수 정의

✔ MAE (Mean Absolute Error)
- 예측값과 실제값의 차이의 절댓값 평균.
- 직관적이며 이상치에 덜 민감한 오차 지표
✔ MSE (Mean Squared Error)
- 예측 오차를 제곱해서 평균낸 값.
- 큰 오차에 민감하며 모델 학습에 자주 사용된다.
✔ RMSE (Root Mean Squared Error)
- MSE의 제곱근, 오차의 실제 단위로 해석 가능.
- 큰 오차에 민감하면서도 해석이 쉬운 지표
✔ RMSLE (Root Mean Squared Logarithmic Error)
- 예측값과 실제값의 로그 차이 제곱 평균의 제곱근.
- 상대적인 오차에 민감하며, 수요 예측에 적합.
🔧 모델링 - 최적의 하이퍼파라미터 찾기 (GridSearchCV)

: GridSearchCV는 머신러닝 모델의 하이퍼파라미터를 최적화하는 방법 중 하나이다.
: 여러 개의 하이퍼파라미터를 조합해보고, 가장 좋은 성능을 내는 조합을 선택 (단, 연산 속도가 느림)
🔧 모델링 - 모델 생성 (Linear / Ridge / Lasso / SGD Regressor)
(Linear Regressor)
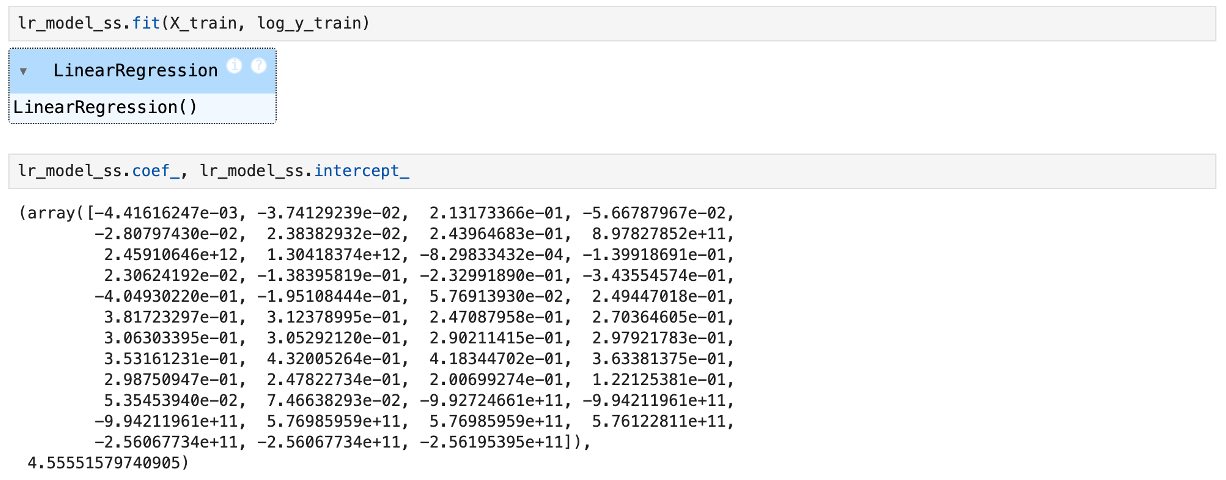
✔ 선형 회귀 모델 훈련
- LinearRegression() 모델을 X_train(훈련 데이터)과 log_y_train(로그 변환된
타깃 변수)으로 학습시켰다.
✔ 회귀 계수(coef_) 및 절편(intercept_) 출력
- coef_
: 학습된 모델의 특성별 회귀 계수(가중치)를 나타낸다.
: coef_ 배열의 각 숫자는 각 특성이 타깃 값에 미치는 영향력을 의미한다.
- intercept_
: 모든 특성이 0일 때 예측되는 값 (절편값)
(Ridge Regressor)
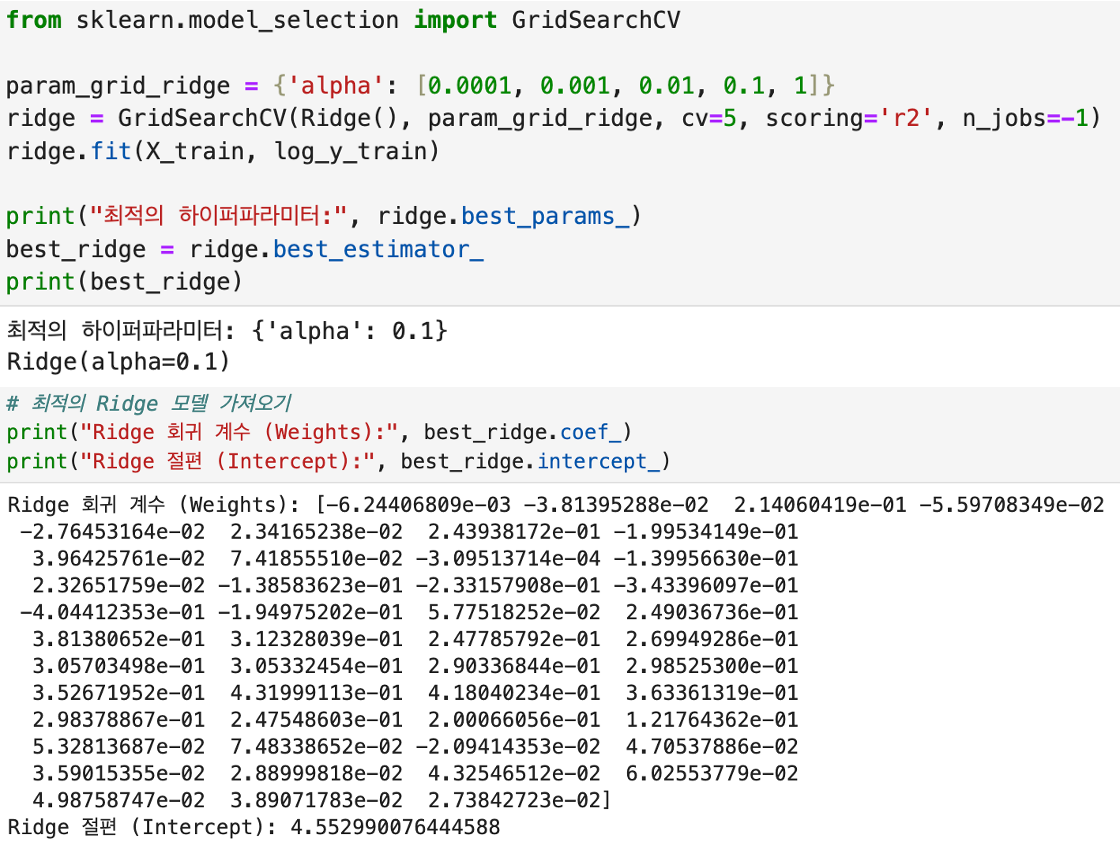
: ridge.best_params_: 최적의 alpha 값을 출력
: best_ridge.coef_: 최적 모델의 가중치 (Feature Weights)
: best_ridge.intercept_: 최적 모델의 절편 (Intercept)
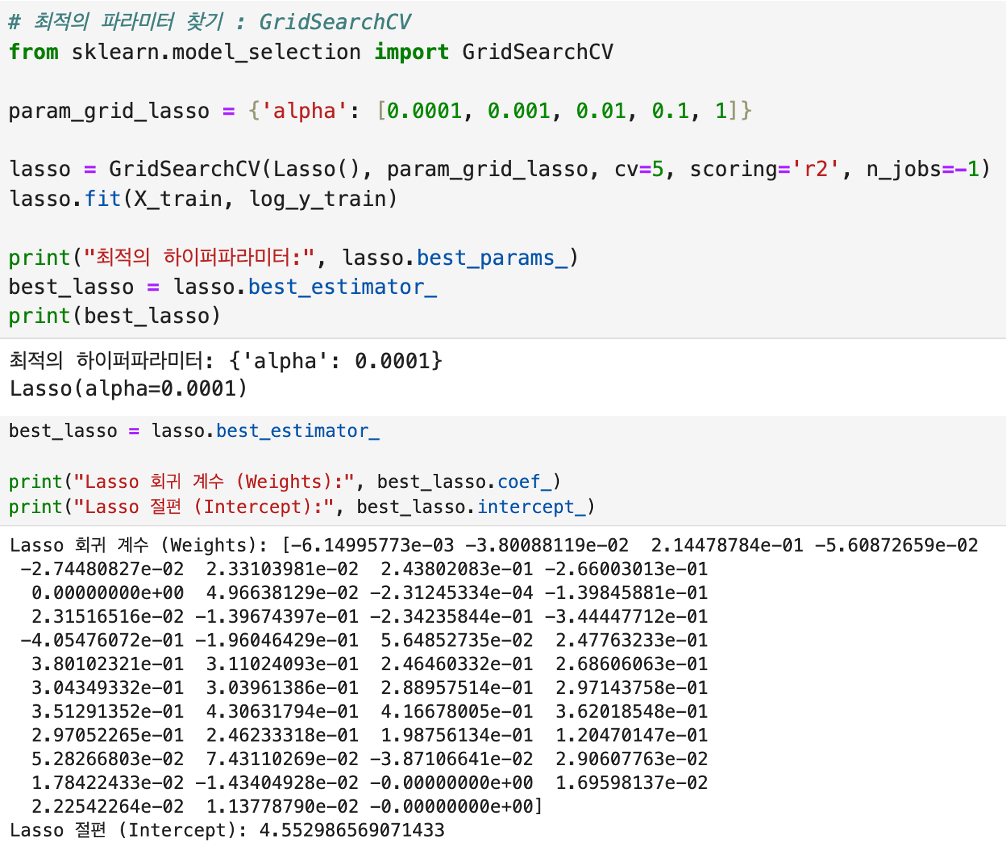
(Lasso Regressor)
(SGD Regressor)

🔧 모델 평가
| 모델 / 평가지표 | R^2 | MAE | MSE | RMSE | RMSLE |
| Linear Regression | 0.8265 | 0.4572 | 0.3853 | 0.6208 | 0.5833 |
| Ridge Regression | 0.826534 | 0.45751 | 0.38522 | 0.62066 | 0.58327 |
| Lasso Regressioin | 0.826533 | 0.45754 | 0.38255 | 0.62069 | 0.58328 |
| SGD Regression | 0.8164 | 0.4712 | 0.4085 | 0.6391 | 0.6008 |
✔ R^2 (결정계수) : 모델의 성능을 나타내는 지표로 1에 가까울수록 좋음
✔ MAE : 오차의 평균 절댓값을 나타내며, 낮을수록 좋음
✔ MSE : 오차를 제곱하여 평균을 낸 값 → 큰 오차가 있을 경우 더 큰 영향을 받음
✔ RMSE : MSE의 제곱근으로, 실제 데이터 단위와 같아 해석에 용이
✔ RMSLE : 로그 변환을 사용한 RMSE로, 상대적 오차를 평가할 때 유용
<성능>
- Linear, Ridge, Lasso 모델은 성능이 거의 동일하게 보여진다.
: 데이터 자체가 선형 관계를 충분히 따르고 있다.
- SGD Regression은 다른 회귀 모델에 성능이 낮게 나타난다.
<최적 모델 선택>
- Linear, Ridge, Lasso 모두 성능 차이가 거의 없으므로, Linear Regression이 가장 간단하고 효율적이다.
- 하지만 과적합이 의심되기에, Ridge Regression 또는 Lasso Regression을 선택하는 것이 바람직하다고 생각한다.
'📗 개인 프로젝트 > 🚲 공유 자전거 수요 예측' 카테고리의 다른 글
| 🚲 공유 자전거 수요 예측 | 4️⃣ 파일 업로드 (0) | 2025.04.21 |
|---|---|
| 🚲 공유 자전거 수요 예측 | 3️⃣ 비즈니스 모델 제안 (0) | 2025.04.21 |
| 🚲 공유 자전거 수요 예측 | 1️⃣ EDA (3) | 2025.04.21 |