
👀 INTRO
목표
: 가장 정확한 분류 모델을 개발하여 고객이 정기 예금을 가입할지 여부를 예측하고, 그 모델을 통해 도출한 인사이트를 바탕으로 비즈니스 전략을 제시하는 것이 이번 프로젝트의 목표이다.
데이터 소개
: UC Irvine Machine Learning Repository에서 제공하는 Bank Marketing 데이터
: 이 데이터는 2008년부터 2010년까지의 은행 마케팅 캠페인 데이터를 포함하고 있다.
| 컬럼명 | 설명 |
| age | 나이 (숫자) |
| job | 직업 (범주형) |
| marital | 결혼 여부 (범주형) |
| education | 교육 수준 (범주형) |
| default | 신용 불량 여부 (범주형) |
| housing | 주택 대출 여부 (범주형) |
| loan | 개인 대출 여부 (범주형) |
| contact | 연락 유형 (범주형) |
| month | 마지막 연락 월 (범주형) |
| day_of_week | 마지막 연락 요일 (범주형) |
| duration | 마지막 연락 지속 시간, 초 단위 (숫자) |
| campaign | 캠페인 동안 연락 횟수 (숫자) |
| pdays | 이전 캠페인 후 지난 일수 (숫자) |
| previous | 이전 캠페인 동안 연락 횟수 (숫자) |
| poutcome | 이전 캠페인의 결과 (범주형) |
| emp.var.rate | 고용 변동률 (숫자) |
| cons.price.idx | 소비자 물가지수 (숫자) |
| cons.conf.idx | 소비자 신뢰지수 (숫자) |
| euribor3m | 3개월 유리보 금리 (숫자) |
| nr.employed | 고용자 수 (숫자) |
| y | 정기 예금 가입 여부 (이진: yes=1, no=0) |
📊 EDA
☑️ 결측치 / 중복값 / 이상치
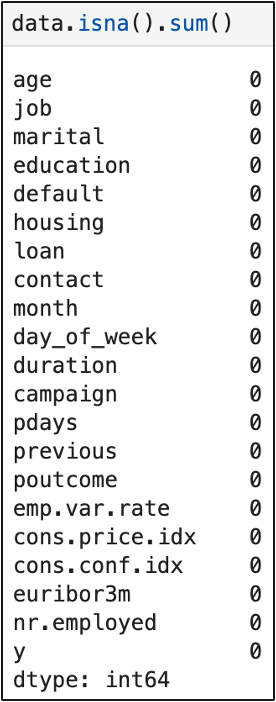
(결측치)
: 결측치 없음
(중복값)
: 중복값 12개 존재 → 제거

(이상치)

: 이상치 존재, 하지만 전체 트리 모델 구조에는 큰 영향이 없다. → 즉, 이상치에 강인함.
: 이상치 제거 전/후, 2가지 모두 시도해보았으나, 모델의 성능이 비슷하므로 최종 모델에서는 이상치 제거 하지 않고 모델링했다.
☑️ 데이터 타입 변환
<'y' 컬럼 데이터타입 변환 (object -> int64)>
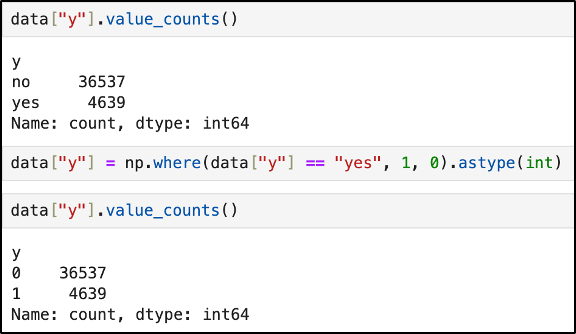

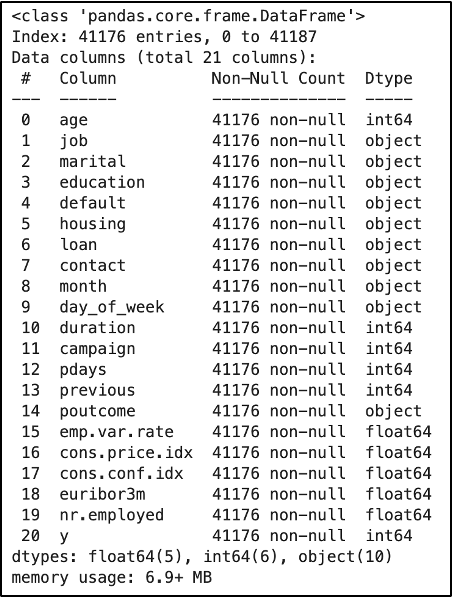
: 처음 데이터를 확인해보니 타깃 변수인 'y' 컬럼이 문자열로 되어 있었다. 하지만 'y'는 예금에 가입했는지 여부를 나타내는 이진 값(0 또는 1)만을 가지므로, 문자열 정보가 전혀 필요하지 않다. 따라서 의미상 더 적합한 int64 타입으로 변환하여, 불필요한 문자열 처리도 피할 수 있고, 모델링 시 타입으로 인한 경고나 오류도 줄일 수 있었다.
☑️ 데이터 분석
<연락 횟수(‘campaign’)에 따른 정기 예금 가입(‘y’) 확률>

- 하강 추세
: 캠페인 횟수가 증가할수록 가입 확률이 감소하는 경향을 보인다. 이는 소비자 피로도나 관심 감소로 인해 반복적인 캠페인이 효과가 줄어드는 것으로 추측된다.
- 최적의 캠페인 횟수
: 약 5~10 회의 캠페인에서 가입 확률이 상대적으로 높은 경향을 보인다. 이 범위 내에서 최적의 캠페인 전략을 취할 필요가 있다.
- 신뢰 구간
: 빨간색 음영 영역은 신뢰 구간을 나타내며, 이 구간이 좁아지면서 캠페인 횟수가 많아질수록 데이터의 변동성이 줄어드는 것으로 보인다.
<연락 횟수(‘campaign’)에 따른 정기 예금 가입(‘y’) 확률>

- len(data[data['pdays'] == 999]) >> 39661
: 경과일 수가 999일은 지난 날짜라기 보다는 특별한 의미가 있는 듯하여 ‘pday_999’ 컬럼을 생성하고 ‘pdays’에는 0으로 변경했다.
- 경과일 수가 증가함에 따라 가입 확률이 일반적으로 증가하는 것으로 보인다.
: 초기에는 가입 확률이 낮지만, 경과일 수가 10일을 넘어서면서 확률이 상승하는 경향이 있다.
- 비선형 패턴
: 가입 확률이 도달하는 특정 값에 따라 시간이 지남에 따라 더 빨리 증가할 수 있음을 시사한다.
<수치형 특성들 간의 상관관계 / ‘y’컬럼과의 상관관계>
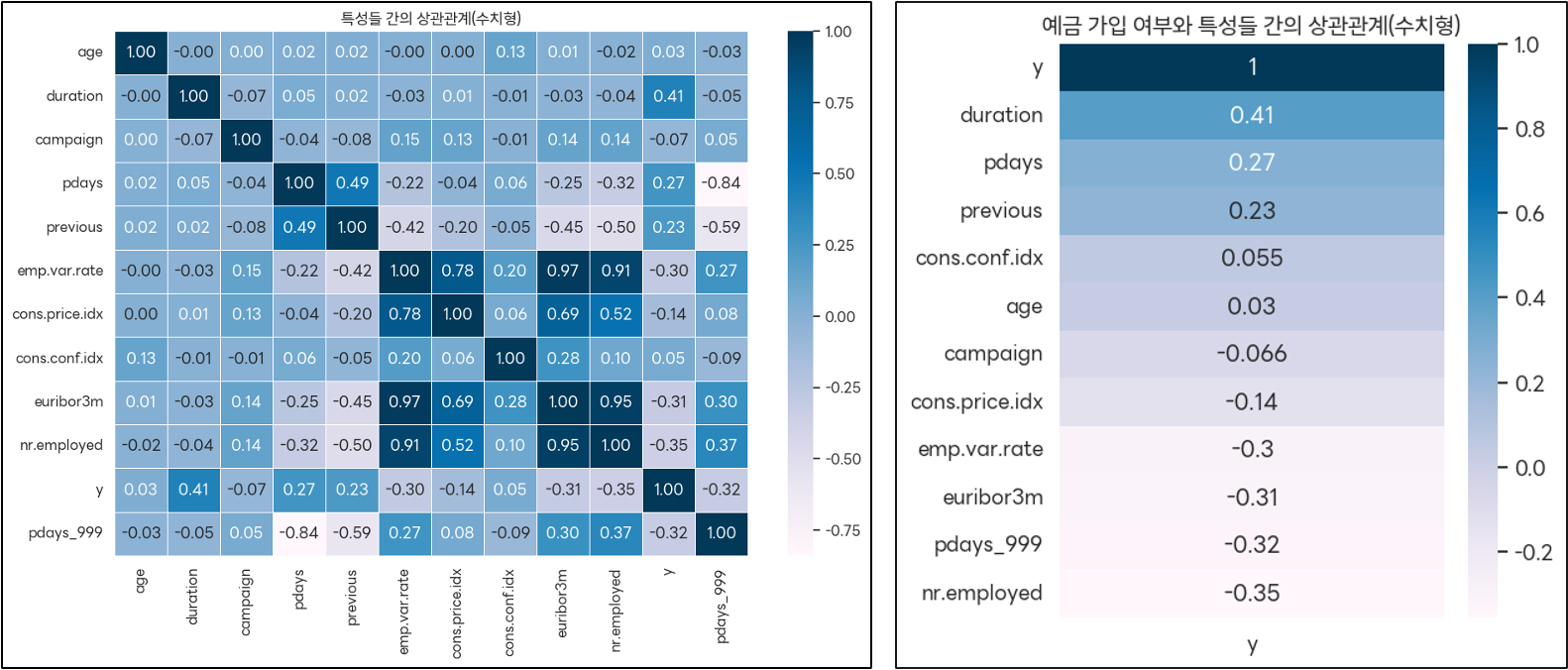
- 'duration'↔'y' : 두 변수 간의 상관계수는 0.41로, 'duration'이 길어질수록 긍정적인 결과(y)에 대한 예측 가능성이 높아진다는 것을 의미함.
- 'pdays'↔'y' : 두 변수 간의 상관계수는 -0.84로, 'pdays' 값이 작을수록 긍정적인 결과(y)에 더 가까워짐을 나타낸다. 즉, 예전 연락이 짧았던 고객이 재방문의 가능성이 더 높다는 의미함.
- 'previous'↔'y' : 상관계수 -0.59로, 이전의 연락 횟수가 많을수록 긍정적인 결과가 낮아짐을 보여준다. 이는 고객이 여러 번 연락을 받았던 경우 결과가 부정적일 수 있음을 나타냄.
- 'pdays'↔'previous' : 두 변수 간의 상관계수 0.49로, 이전 연락이 많았던 경우 'pdays' 값이 더 높을 수 있음을 알 수 있음.
- ‘emp.var.rate'↔'cons.price.idx' : 각각 다른 경제 지표로, 양의 상관관계를 가지며(상관계수 0.78) 서로 긍정적인 영향을 미칠 수 있음을 알 수 있고, 경제 지표가 안정적일수록 소비자 신뢰도 또한 높아질 가능성이 있음.
- 'campaign'의 상관관계는 상대적으로 낮은 편이며(최대 0.15) 캠페인의 효과가 다른 변수들에 비해 뚜렷하지 않음을 나타냄.
<PI Chart : 컬럼의 카테고리별 비율 / Stack Bar Chart : 예금 가입 여부별 비율>
('job' 컬럼)

: 소득이 낮거나 불안정한 직업군에서 가입률이 상대적으로 높다. → 예금 상품의 안정성이 어필된 것일 수 있다.
('contact' 컬럼)
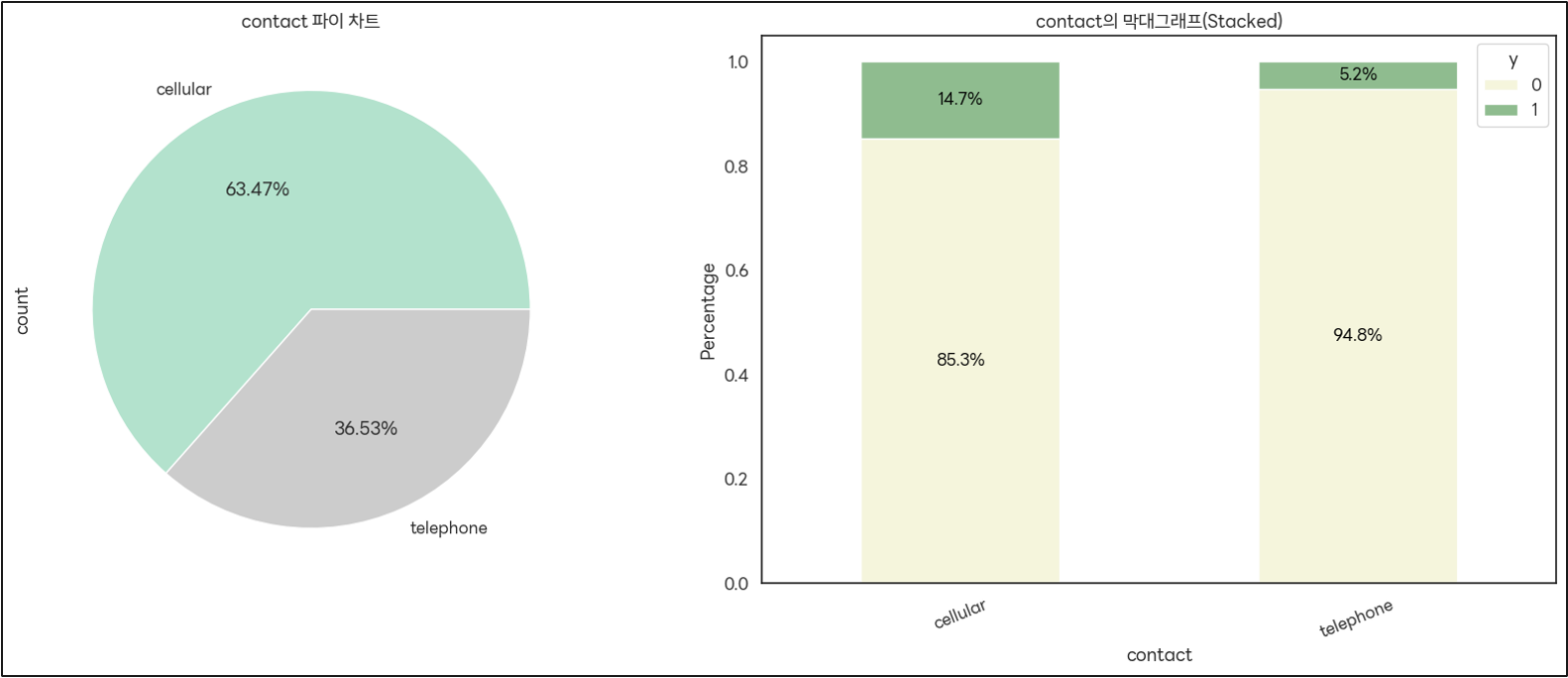
: cellular로 연락한 경우 가입률이 더 높다. → 마케팅 채널로 cellular 활용이 효과적일 수 있다.
('poutcome' 컬럼)
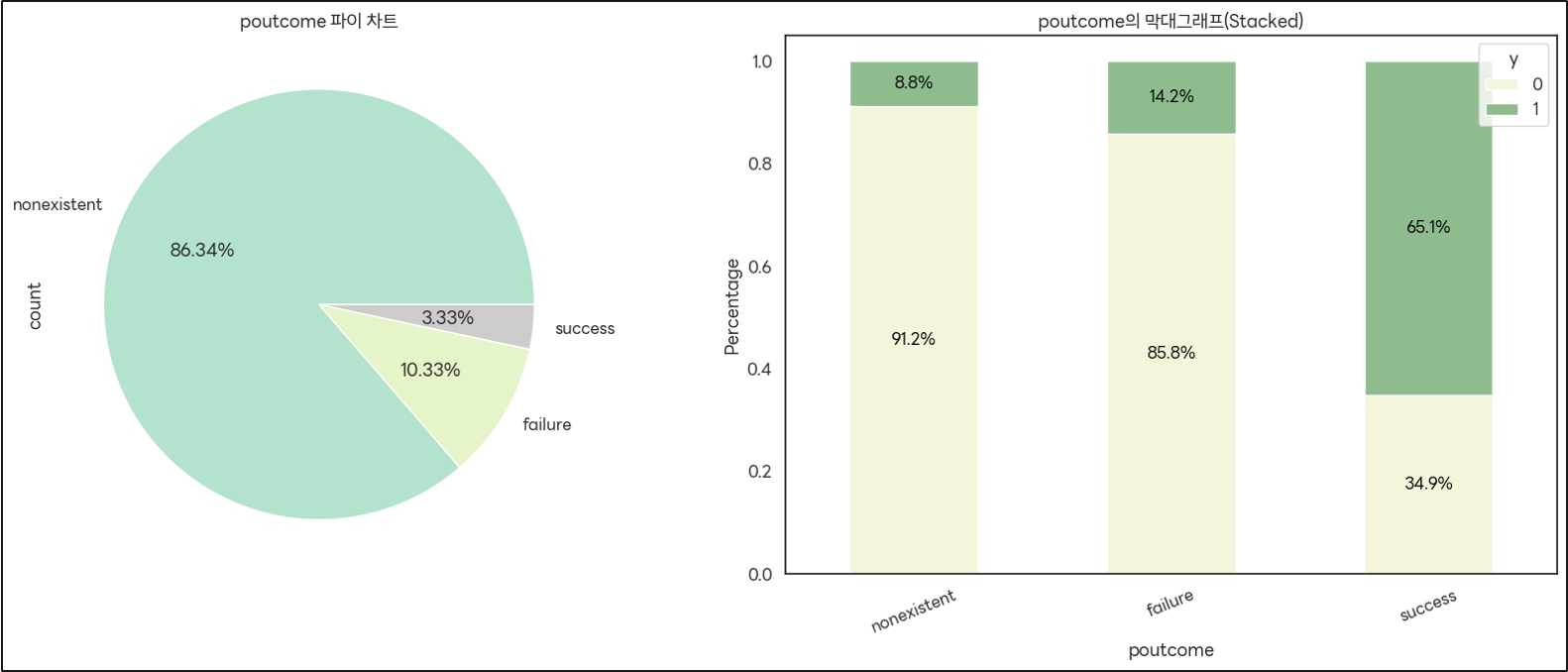
: 과거 마케팅에 성공한 고객에게 재접촉하면 가입 가능성이 높음.
<PI Chart : 컬럼의 카테고리별 비율 / Stack Bar Chart : 예금 가입 여부별 비율>

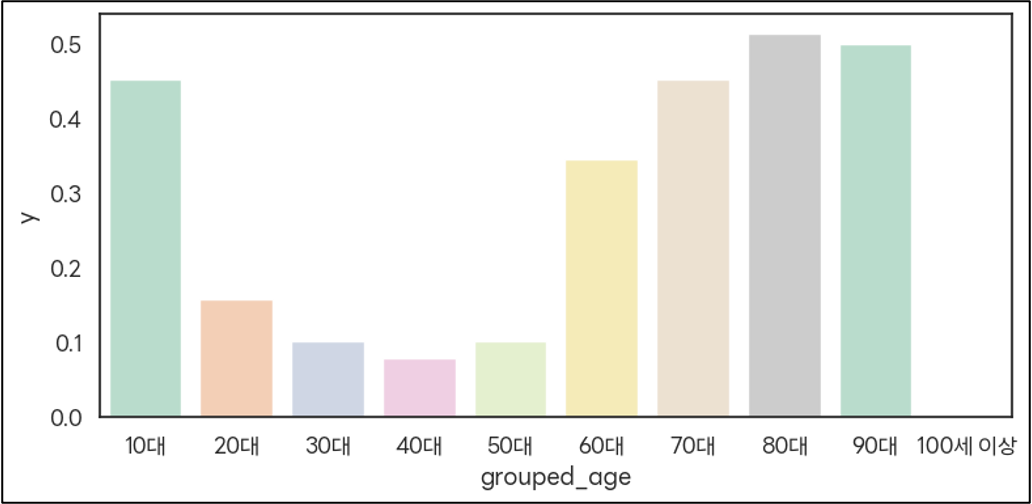
: 10대, 70대, 80대, 90대에서 가입률이 높다. (약 45~52%)
: 젊은 층(10대)과 고령층(70대 이상)에서 예금 상품에 대한 관심이 높다. → 각 세대에 맞는 마케팅 전략 필요
☑️ Feature Engineering
('job' 컬럼 그룹화)

: 카테고리 개수가 많아 모델학습에 불리하게 작용할 수 있기에 그룹화해서 카테고리 개수를 줄였다.
'📗 개인 프로젝트 > 🏦 정기 예금 가입 여부 예측' 카테고리의 다른 글
| 🏦 정기 예금 가입 여부 예측 | 4️⃣ 파일 업로드 (0) | 2025.04.21 |
|---|---|
| 🏦 정기 예금 가입 여부 예측 | 3️⃣ 비즈니스 전략 제안 (0) | 2025.04.21 |
| 🏦 정기 예금 가입 여부 예측 | 2️⃣ 모델링 (0) | 2025.04.21 |